Higher beings, these words are for you alone. Občas tu je něco blbě tak bacha

Spolupachatel skript Hanek Javatý.

Balls

Odhady

[P: chapter 1, MN: chapter 3]

Odhady faktoriálů

Definice: Faktoriál

$n! \overset{def}{=} n \cdot (n - 1) \cdot (n - 2) \cdot \dots \cdot 2 \cdot 1$

Pozorování

$(\forall n \in ℕ_{0}) (n! \leq n^{n})$

Důkaz

Nejdříve dokážeme AG nerovnost, kterou použijeme při důkazu tvrzení níže. Actually that was a lie ale nechám to tady jelikož už sem to vy $a s c i i m a t h$ oval.

Pozorování

AG nerovnost $\forall x, y \in ℝ \geq 0$

$\sqrt{x y} \leq \frac{x + y}{2}$

Důkaz

$\begin{matrix} {(\sqrt{x} - \sqrt{y})}^{2} & \geq & 0 \\ x - 2 \sqrt{x y} + y & \geq & 0 \\ x + y & \geq & 2 \sqrt{x y} \\ \frac{x + y}{2} & \geq & \sqrt{x y} \\ ✨ \end{matrix}$

Pozorování

$(\forall n \in ℕ \geq 0) (n^{\frac{n}{2}} \leq n! \leq n^{n})$

Důkaz

$n!^{2} = (n \cdot 1) \cdot ((n - 1) \cdot 2) \cdot ((n - 2) \cdot 3) \cdot \dots \cdot (1 \cdot n)$

Každý z těchto činitelů $c_{i} \geq n$ , $c_{i} = i \cdot (n - i + 1)$ . To protože na okrajích $i = 1$ nebo $i = n$ je to zjevně $n$ .

V intervalu $i \in {2, n - 1}$ je $\min (i, n - i + 1) \geq 2$ a $\max (i, n - i + 1) \geq \frac{n}{2}$

tudíž

$n!^{2} \geq n^{n}$

$n! \geq n^{\frac{n}{2}}$

Nyní ta těžší nerovnost

Pozorování

$\forall n \in ℕ \geq 0$

$e {(\frac{n}{e})}^{n} \leq n! \leq e n {(\frac{n}{e})}^{n}$

Důkaz

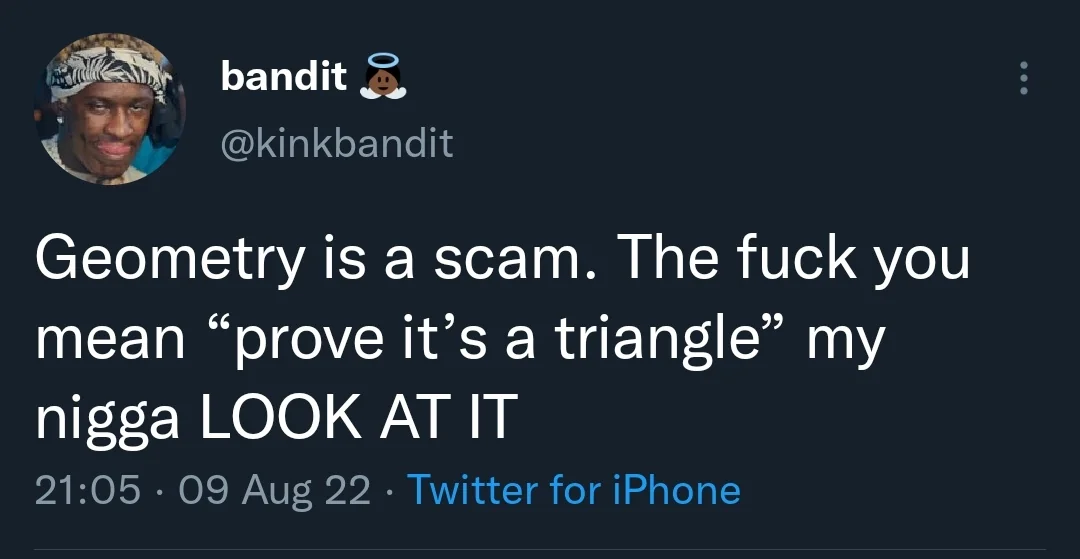
Předem se omlouvám, je to convoluted AF. Obrázek je důležitej, vlastně zavíráme $\ln (n!)$ mezi dva integrály $\ln (n!)$ co má jiný meze.

Spodní odhad. Pojďme se podívat na to, jak se chová funkce $\ln (n!)$ .

$\ln (n!) = \sum_{i = 1}^{n} \ln (i) =$ modrá část.

$\ln (n!)$ tedy odpovídá modré části. Ta je určitě větší než červená, což je integrál $\ln x$ od $1$ do $n$ .

Červená:

$\int_{1}^{n} \ln (x) 𝑑 x = {[x \cdot \ln x - x]}_{1}^{n} = n \ln n - n + 1$

Můžeme z logaritmu udělat výsledek itegrálu tím hodnotu zmenšit. $n! = e^{\ln (n!)} \geq e^{n l n n - n + 1} = n^{n} \cdot \frac{1}{e^{n}} \cdot e = e {(\frac{n}{e})}^{n}$

K dokázání horního odhadu nám pomůže zelená část. Je vlastně stejná jako ta modrá, akorát je posunutá doprava. Pokud budeme porovnávat její hodnotu s červenou částí, tak červená bude větší, musíme ji ale také posunout. Integrál bude tedy od $1$ do $n + 1$

$\ln (n!) \leq \int_{1}^{n + 1} ln (x) d x = {[x cdot lnx - x]}_{1}^{n + 1}$ $= (n + 1) \ln (n + 1) - n$

$n! = e^{\ln} (n!) \leq e^{n + 1} \ln (n + 1) - n = \frac{{(n + 1)}^{n + 1}}{e^{n}}$

Nyní opět evil matematický dosazení aby nám vyšlo to co chceme. Za $n$ dosadíme $n - 1$ .

$n! = n \cdot \underset{(dis one)}{\underset{⏟}{(n - 1)!}} \leq n \cdot (\frac{n^{(n)}}{e^{n - 1}}) = e n {(\frac{n}{e})}^{n}$

Celkově tedy

$e {(\frac{n}{e})}^{n} \leq n! \leq e n {(\frac{n}{e})}^{n}$ 🔲

Pozorování

Stirling formula $n! ≅ (2 pin) \frac{1}{2} {(\frac{n}{e})}^{n}$

Důkaz

Patří do analýzy nebo tak něco

Odhady binomického koeficientu

Definice: Binomický koeficient

$([n], [k]) = \frac{n!}{k! (n - k)!} = \frac{n \cdot (n - 1) \cdot \dots \cdot (n - k + 1)}{k!}$

Pozorování

${(\frac{n}{k})}^{k} \leq ([n], [k]) \leq {(\frac{e n}{k})}^{k}$

Důkaz

Spodní odhad

$(\forall i \in {0, \dots, k - 1}) (\frac{n - i}{k - i} \geq \frac{n}{k})$

(důkaz roznásobením). Díky tomu

$([n], [k]) o v e r s e t (def) (=) \prod_{i = 0}^{k - 1} \frac{n - i}{k - i} \geq \prod_{i = 0}^{k - 1} \frac{n}{k} = {(\frac{n}{k})}^{k}$

Horní odhad

Nechť $x = \frac{k}{n}$ . Všimni si že $0 \leq x \leq 1$ protože $k \leq n$

Budiž vymyšlený výraz:

$([n], [0]) x^{0} + ([n], [1]) x^{1} + \dots + ([n], [n]) x^{n} = {(1 + x)}^{n}$

Na levé straně vynecháme sčítance za $x^{k}$

$([n], [0]) x^{0} + ([n], [1]) x^{1} + \dots + ([n], [k]) x^{k} \leq {(1 + x)}^{n}$

Vydělíme $x^{k}$

$\frac{1}{x^{k - 0}} ([n], [0]) + \frac{1}{x^{k - 1}} ([n], [1]) + \dots + \frac{1}{x^{k - k}} ([n], [k]) \leq \frac{{(1 + x)}^{n}}{x^{k}}$

Na levé straně je každý koeficient $\geq 1$ , takže když je vynecháme tak stranu pouze zmenšíme.

$([n], [0]) + ([n], [1]) + \dots + ([n], [k]) \leq \frac{{(1 + x)}^{n}}{x^{k}}$

Všimni si cool feature je že už tam je ten $([n], [k])$ který chceme! Expandujeme $x = \frac{k}{n}$ .

$([n], [0]) + ([n], [1]) + \dots + ([n], [k]) \leq {(1 + \frac{k}{n})}^{n} \cdot {(\frac{n}{k})}^{k}$

(všimni si obrácení zlomku $\frac{k}{n}$ kterým dělíme)

využijeme fakt: $1 + x \leq e^{x}$ ( $\to 1 + \frac{k}{n} \leq e^{\frac{k}{n}}$ ) pro umlácení pravé strany:

${(1 + \frac{k}{n})}^{n} \leq {(e^{\frac{k}{n}})}^{n} = e^{k}$

tedy dostaneme

$([n], [0]) + ([n], [1]) + \dots + ([n], [k]) \leq e^{k} \cdot {(\frac{n}{k})}^{k}$

Vlevo zahodíme Binomické koeficienty které nás nezajímají (zase pouze zmenší)

$([n], [k]) \leq {(\frac{e n}{k})}^{k}$

🔲

Nyní se podívejme co se děje s prostředním binomickým koeficientem, ten by měl být řekněme největší (něco něco pascalův trojúhelník);

Pozorování

$\frac{2^{2 m}}{2 \sqrt{m}} \leq ([2 m], [m]) \leq \frac{2^{2 m}}{\sqrt{2 m}}$

Důkaz

Nejdříve si pořiďme $P$ . $P \overset{def}{=} \frac{1 \cdot 3 \cdot 5 \cdot \dots \cdot (2 m - 1)}{2 \cdot 4 \cdot 6 \cdot \dots \cdot (2 m)}$ Vynásobíme $1$ $P = \frac{1 \cdot 3 \cdot 5 \cdot \dots \cdot (2 m - 1)}{2 \cdot 4 \cdot 6 \cdot \dots \cdot (2 m)} \cdot \frac{2 \cdot 4 \cdot \dots \cdot (2 m)}{2 \cdot 4 \cdot \dots \cdot (2 m)}$ $= \frac{(2 m)!}{2^{2 m} \cdot {(m!)}^{2}}$ $= \frac{1}{2^{2 m}} \cdot ([2 m], [m])$ To nám pomůže, protože v dokazované nerovnosti jsou v čitatelích právě $2^{2 m}$ , takže nyní nám stačí dokázat $\frac{1}{2 \sqrt{m}} \leq P \leq \frac{1}{\sqrt{2 m}}$

Horní odhad

Uvažme posloupnost $(\frac{3}{2^{2}}) \cdot (\frac{3 \cdot 5}{4^{2}}) \cdot (\frac{5 \cdot 6}{6^{2}}) \cdot \dots \cdot \frac{(2 m - 1) (2 m + 1)}{{2 m}^{2}}$ , ta má ve výsledku v čitateli (skoro) všechna lichá čísla dvakrát a všechna sudá čísla ve jmenovateli dvakrát. Tado posloupnost se tedy rovná $P^{2}$ až na přebytek. Co zbývá? $1$ vlevo a $2 m + 1$ vpravo. $= (2 m + 1) P^{2}$ Jelikož každý činitel $< 1$ , tak dostáváme že $(2 m + 1) P^{2} < 1$ , tedy $P^{2} \leq \frac{1}{2 m + 1}$ Zmenšíme jmenovatel, takže zvětšíme pravou stranu. $P^{2} \leq \frac{1}{2 m}$ $P \leq \frac{1}{\sqrt{2 m}}$

Spodní odhad je podobný, ale má obrácené čitatele a jmenovatele. Uvažme posloupnost $(\frac{2 \cdot 4}{3^{2}}) \cdot (\frac{4 \cdot 6}{5^{2}}) \cdot (\frac{6 \cdot 8}{7^{2}}) \cdot \dots \cdot \frac{(2 m - 2) (2 m)}{{2 m - 1}^{2}}$ , Tato posloupnost se chová skoro stejně jako $\frac{1}{P^{2}}$ , až na přebytek v čitateli. Co přebývá? $2$ vlevo a $2 m$ vpravo. Tudíž $= \frac{1}{2 \cdot (2 m) \cdot P^{2}}$ Každý člen je opět $< 1$ , takže $\frac{1}{2 \cdot (2 m) \cdot P^{2}} < 1$ $P^{2} > \frac{1}{2 \cdot 2 m}$ $P > \frac{1}{2 \sqrt{m}}$ 🔲

Příklad: random walk. Kolikrát v průměru se dostaneme po 2m krocích zpátky do počátku, jestliže se v každém kroku rozhodneme jít náhodně doleva/doprava?

Řešení: po $2 m$ krocích existuje $([2 m], [m])$ procházek které končí v 0. Celkem je tedy pravděpodobnost $\frac{([2 m], [m])}{2^{2 m}}$ že po $2 m$ krocích jsme v nule. Suma přes všechny délky:

$\sum_{m = 1}^{(\infty)} \frac{([2 m], [m])}{2^{2 m}} \geq \sum_{m = 1}^{(\infty)} \frac{1}{2 s q r t m}$ což diverguje. Po nekonečně krocích tedy můžeme očekávat nekonečně návšťev počátku.

Divergence se může ověřit vytáhnutím $\frac{1}{2}$ ven a omezení harmonickou řadou.

Vytvořující funkce

Motivační příklad, kolika způsoby jde vytáhnout 7 míčků z pytle ve kterém jsou 3 červené, 4 zelené a 5 modrých? Moudrý čtenář ví že je to konvoluce $(x + x^{2} + x^{3}) (x + \dots + x^{4}) (x + \dots + x^{5})$ a ptáme se na koeficient $x^{7}$ .

Definice: Vytvořující funkce (VF)

Nechť je ${(a_{n})}_{n = 0}^{\infty}$ posloupnost reálných čísel. Vytvořující funkce této posloupnosti je řada $a (x) = \sum_{i = 0}^{\infty} a_{i} x^{i}$

Poznámka: Spíše než nekonečná řada je důležitá uzavřená reprezentace vytvořující funkce. Např. řada $a (x) = 1 + x + x^{2} + \dots$ je generovaná funkcí $\frac{1}{1 + x}$ . Pokud je $x$ v intervalu $(- 1, 1)$ , tak řada konverguje a má stejný součet. (Důkaz taylorova řada).

Z toho dostáváme jakousi podmínku pro to, aby posloupnost měla vytvořující funkci. Stačí, aby $| a_{n} | \leq K^{n}$ pro nějaké reálné $K$ a $A A n \to 1$ . Pak totiž pro $\forall x \in (- \frac{1}{K}, \frac{1}{K})$ řada $a (x) = \sum_{i = 0}^{(\infty)} a_{i} x^{i}$ konverguje.

Zajímavé je co se stane, když do VF dosadíme 0. V tu chvíli dostaneme první prvek $a_{0}$ , protože všechny ostatní se vynulují. Také je zajímavé derivovat VF. Tím se všechny členy posloupnosti posunou o jedna doleva a vydělí se předchozím exponentem. Kombinací těchto dvou faktů dostáváme vzorec pro $n$ -tý člen posloupnosti. Uděláme $n$ -tou derivaci, vydělíme $n!$ a dosadíme $0$ .

$a_{n} = \frac{a^{(n)} (0)}{n!}$

Definice: Tabulka operací s VF

Operace	Řada	Úprava
Součet	$a_{0} + b_{0}, a_{1} + b_{1}, a_{2} + b_{2}, \dots$	$a (x) + b (x)$
Násobek	$α a_{0}, α a_{1}, α a_{2}, \dots$	$α a (x)$
Posun doprava	$0, a_{0}, a_{1}, \dots$	$x \cdot a (x)$
Posun doleva	$a_{1}, a_{2}, a_{3}, \dots$	$\frac{a (x) - a_{0}}{x}$
Substituce $α x$	$α^{0} a_{0}, α^{1} a_{1}, α^{2} a_{2}, \dots$	$a (α x)$
Substituce $x^{n}$	$a_{0}, \overset{n - 1}{\overset{⏞}{(0, \dots, 0)}}, a_{1}, \overset{n - 1}{\overset{⏞}{(0, \dots, 0)}}, a_{2}, \dots$	$a (x^{n})$
Derivace	$a_{1}, 2 a_{2}, 3 a_{3}, \dots$	$a' (x)$
Integrování	$0, a_{1}, \frac{a_{2}}{2}, \frac{a_{3}}{3}, \dots$	$\int_{0}^{x} a (t) 𝑑 t$
Konvoluce	$a_{n} = \sum_{k = 0}^{n} (a_{k} \cdot b_{n - k})$	$a (x) \cdot b (x)$

Ověř si to :)

Teď dlouhej talk o tom jak vyjádřit uzavřeně nějakou hodnotu rekurentně zadané rovnice. Tldr: Zapiš si posloupnost jako řadu, vypiš prvních pár prvků abys tam měl ten člen co máš rekurentně zadanej.

$a_{n + 2} = a_{n + 1} + 2 a_{n}$

$a (x) = a_{0} + a_{1} x + x^{2} \sum_{n = 0}^{(\infty)} a_{n + 2} x^{n}$

Všimni si pár triků, např vytknutí $x$ před sumu. Poté dosaď rekurenci, roztrhni sumu a snaž se nekonečnou sumu nahradit za tvou VF. Neboj se podvádět, musíš přičítat nulté a první členy, zvracej $x$ zpátky do sumy, prostě se snaž dostat tvar $\sum_{n = 0}^{(00)} a_{n} x^{n}$ . To pak nahraď za $a (x)$ a vyřeš pro $a (x)$ .

Potom dostaneš uzavřený tvar pro tvojí VF. Dostaň ji do tvarů $\frac{a}{1 - x} +$ to samé několikrát, kde $x$ není nutně $x$ a $a$ je konstanta. Nejspíš budeš řešit parciální zlomky. Pak se podívej do tabulky, vyhaluz posloupnosti co sčítáš a máš vzoreček pro $a_{n}$ . Snadné, že? :)

Přikládám svůj úkol protože si to nebudu pamatovat :)/

Zobecněná binomická věta

Definice: Zobecněný binomický koeficient

$\forall r \in ℝ, \forall k \in ℕ_{0}$

$([r], [k]) = \frac{r (r - 1) (r - 2) \dots (r - k + 1)}{k!}$

Prostě normální koeficient :)

Definice: Zobecněná binomická věta

$\forall r \in ℝ, x \in (- 1, 1)$

${(1 + x)}^{r} = ([r], [0]) x^{0} + ([r], [1]) x^{1} + \dots$

Z toho plyne, že pro $n \in ℕ, x \in (- 1, 1)$

$\frac{1}{{1 - x}^{n}} = ([n - 1], [n - 1]) x^{0} + ([n], [n - 1]) x^{1} + ([n + 1], [n - 1]) x^{2} + \dots =$ $= \sum_{i = 0}^{\infty} ([n + i - 1], [n - 1]) x^{i}$

Příklad: jak spočítat motivační příklad ale lépe.

V krabici je 30 červených, 40 žlutých a 50 zelených míčků. Kolika způsoby lze vybrat 70?

$(1 + x + \dots x^{30}) (1 + x + \dots + x^{40}) (1 + x + \dots + x^{50}) =$

$= \frac{1 - x^{31}}{1 - x} \frac{1 - x^{41}}{1 - x} \frac{1 - x^{51}}{1 - x}$

Wait, cože? <- tohle bys měl být ty. Jak jsme přišli na to že $1 + x + \dots + x^{30}$ je nějakej random zlomek? Vem vytvořující funkci samých 1 a vynásob jí $1 - x^{31}$ .

$\frac{1}{1 - x} - \frac{x^{31}}{1 - x} = \frac{1}{1 - x} \cdot (1 - x^{31})$

Co dostaneš? Normální vytvořující funkci ( $\cdot 1$ ), od které ale odečítáš posunutou VF od $x^{31}$ . To znamená že ti zbyde jen $1 + x + \dots + x^{30}$ .🪄

To ale znamená že máme funkci v uzavřené formě, a díky zobecněné binomické větě víme, že

$= (([2], [2]) + ([3], [3]) x + \dots) (1 - x^{31}) (1 - x^{41}) (1 - x^{51})$

A ptáme se na koeficient u $x^{70}$ , který $=$

$([72], [2]) +$ za samé 1, $- ([72 - 31], [2]) +$ když vybereme $x^{31}$ atd…

Definice: Zakořeněný binární strom

Strom je buď prázdný, nebo má levý a pravý podstrom, které jsou také binárními stromy (můžou být prázdné)

Budeme počítat kolik jich je, $b_{n} =$ počet různých binárních zakořeněných stromů na n vrcholech.

Lze si rozmyslet že $b_{n} = \sum_{k = 0}^{n - 1} b_{k} \cdot b_{n - k - 1}$ , protože se rekurzíme na obě části, do každé přiřadíme část vrcholů. Když z toho uděláme VF, tak vychází, že

$b (x) = x \cdot b (x) \cdot b (x) + 1$

$+ 1$ aby vycházelo $b (0)$ správně a $x$ je posun. Pak už je to pouze konvoluce. Vyjádříme $b (x)$ 🪄 - normální kvadratická rovnice. Na odmocninu použij zobecněnou binomickou větu (mocníš na $\frac{1}{2}$ ).

$b (x) = \frac{- \sum_{k = 1}^{(\infty)} {(- 4)}^{k} ([\frac{1}{2}], [k]) x^{k}}{2 x}$

Vyjádření konkrétního koeficientu pak dává Catalanovo číslo

$b_{n} = \frac{1}{n + 1} ([2 n], [n])$

TODO #partitions of n into odd parts = #partitions of n into distinct parts [MN 12.7 / here]

Finite projective planes (fpp FPR)

[P: chapter 3, MN: chapter 9]

Definice: množinový systém

budiž:

$X$ množina
$S \subseteq b b b P (X)$ (některé podmnožiny $X$ )

Množinový systém je dvojice $(X, S)$

Definice: Konečná projektivní rovina (FPR)

Jako kdyby $ℝ^{2}$ ale very nice✨ and neat✨ and all✨ (máme rádi FPR)

$X$ je množina bodů. $c c L$ je množina čar. $(X, c c L)$ je množinový systém.

Existují 4 různé body takové že libovlná přímka protne maximálně 2 z nich.
Libovolné 2 přímky mají právě jeden společný bod
Libovolné 2 body mají právě jednu společnou přímku

Pozorování

Nechť $(X, c c L)$ FPR.

Všechny přímky mají stejný počet bodů.

Důkaz

Vemme libovolné $L, L' \in c c L$ . Nejprve pomocné pozorování:

Pozorování

Existuje bod $z \in X$ který není ani na $L$ ani na $L'$

Důkaz

Vezmeme 4-prvkovou množinu $F$ z prvního axiomu. Máme $| L \cup F | \leq 2$ a $| L' \cup F | \leq 2$ .

Pokud $F$ není podmnožina $L \cup L'$ pak máme hotovo. Znamená to že alespoň jeden bod z $F$ je mimo $L$ i $L'$ .

Jinak musí $L$ protínat $F$ ve 2 bodech $a$ a $b$ a zároveň musí $L'$ protínat $F$ ve druhých 2 bodech $c$ a $d$ (více by bylo ve sporu s axiomem) ( $F = {a, b, c, d}$ ).

Pak vezmeme přímky:

$R_{1}$ protíná $a$ a $c$
$R_{2}$ protíná $b$ a $d$

Nechť $z$ je průnik $R_{1}$ s $R_{2}$ . Pak $z$ není v $L$ ani v $L'$ .

$L$ a $R_{1}$ se protínají v bodě $a$ . Pokud by $z$ byl v $L$ pak by se $L$ a $R_{1}$ protínají v bodech $z$ i $a$ což je spor. Tudíž $z$ nemůže ležet na $L$ a analogicky ani na $L'$ . 🔲

Ozbrojeni tímto pozorováním, $L$ a $L'$ mají stejnou velikost, definujíc funkci $v a r p h i : L \to L'$ .

Ukážeme, že $v a r p h i$ je bijekce.

Neformálně: $z$ je náš sniping spot a $x \in L$ jsou body skrz které střílíme do $L'$ .

Vemme náš shiny bod $z$ mimo $L \cup L'$ a definujme obraz (terč) $v a r p h i (x)$ pro $x \in L$ jako průnik $L'$ s přímkou která prochází body $x$ a $z$ (bullet trail).

Z axiomů 2 a 3 je terč dobře definovaný. Dvě různá $x, y \in L$ musí mít různé obrazy $varphi(x), $v a r p h i (y)$ jinak by tyto dva bullet traily (přímky) sdílely více než jeden bod. Tudíž $v a r p h i$ je bijekce.

Definice: Řád FPR

Řád FPR $(X, c c L)$ je $| L | - 1$ pro libovolné $L \in c c L$ (všechny $L$ jsou stejně dlouhé).

(To $- 1$ je lehce otravné ale není to chyba…)

Pro FPR $(X, c c L)$ řádu $n$ :

Pozorování

Právě $n + 1$ přímek prochází každým bodem $x$

Důkaz

Nechť libovolný $x \in X$ . Jistě máme $L \in c c L$ která neobsahuje $x$ .

Pro každý $y \in L$ vezmeme přímku procházející $x$ a $y$ . To je jistě přímka a jistě prochází $x$ a jistě jich je $n + 1$ . Nice.

Ale co kdyby existovala nějaká další zlá přímka $Z$ ? Taková by musela protnout $x$ ale zároveň každé 2 přímky mají společný bod takže existuje $z \in Z \cup L$ takže $z$ je jedno z $y$ a žádná zlá přímka $Z$ neexistuje.

Pozorování

$| X | = n^{2} + n + 1$

Důkaz

Vezmeme $L = {x_{0}, \dots, x_{n}} \in c c L}$ a bod $a$ mimo $L$ . Pak vyrobíme přímky $L_{0}, \dots L_{n}$ kde $L_{i}$ protíná $a$ a $x_{i}$ . Každá $L_{i}$ má $n$ dalších bodů mimo $a$ , takže dohromady $n + 1$ přímek obsahuje $n$ různých bodů plus samotné $a$ . $(n + 1) \cdot n + 1 = n^{2} + n + 1$ .

(Jednotlivá $L_{i}$ nemohou sdílet těchto “ $n$ dalších bodů” protože pak by tyto 2 přímky sdíleli 2 body ( $a$ a tento jeden další))

Pozorování

$| c c L | = n^{2} + n + 1$

Důkaz

Důkaz vypadne automaticky z toho minulého po researchnutí duality.

Dualita

Definice: Dualita

Dualita znamená “prohození role přímky a bodu”. Pro přesnou formulaci si pro FPR zavedeme graf incidence.

Definice: Graf incidence

Bipartitní graf kde v první partii vrcholy reprezentují přímky a v druhé partii vrcholy reprezentují body.

Mezi vrcholi je hrana pokud daný bod patří do dané přímky.

Pro dané FPR $(X, c c L)$ jeho duál $(X', c c L')$ dostaneme vyrobením grafu incidence, prohozením významu partií a přeinterpretováním transformovaného bipartitního grafu incidence zpět na FPR.

Pozorování

Duál FPR je také FPR

Důkaz

Budiž FPR $(X, c c L)$ a jeho duál $(c c L, Λ)$ , kde $Λ$ je systém podmnožin $c c L$ . Každý z těchto podmnožin odpovídá nějakému bodu z $X$ .

Všimněte si, že pro různé $x \in X$ dostaneme různé podmnožiny $c c L$ .

Musíme ověřit axiomy FPR pro tento duál.

Přeloženo pro duál říká: Existují 4 přímky takové že žádné 3 z nich nemají společný bod. Vezmeme ${a, b, c, d}$ z původního axiomu pro neduál. Z něj vyrobíme 4 přímky: $L_{1} = a b$ , $L_{2} = c d$ , $L_{3} = a d$ , $L_{4} = b c$ . Pro tyhle to platí.
Je to samé jako 3. pro neduál!
Je to samé jako 2. pro neduál!

Pozorování

Duál FPR řádu $n$ je FPR řádu $n$

Důkaz

plyne z pozorování o počtu bodů na přímce a přímek procházející bodem

Pozorování

Existují FPR řádu 2, 3, 4, 5. 6 ne. 7, 8, 9 existují, 10 ne.

Existují pokud existuje těleso řádu $n$ (tedy $n = p^{α}$ pro prvočíslo $p$ ).

Konstrukce FPR z konečného tělesa.

Prohlásíme že existují trojice prvků z tělesa.
Budiž ekvivalence $\approx$ kde trojice $(a, b, c) \approx (d, e, f)$ kdyžž existuje nenulová $λ$ z tělesa taková že $a = λ d$ , $b = λ e$ , $c = λ f$ .
Body v FPR jsou třídy této ekvivalence KROM $(0, 0, 0)$ . (Takhle vyrobené FPR se často značí $P K^{2}$ kde $K$ je to původní těleso)
Přímky v tomto FPR jsou opět trojice prvků z tělesa bez $(0, 0, 0)$ .
Bod $(x, y, t)$ leží na přímce $(a, b, c)$ kdyžž $a x + b y + c t = 0$ .
Profit

Stačí dokázat axiomy:

Pozorování

Začneme s tím že 2 přímky sdílí právě 1 bod.

Důkaz

Nechť máme $(a_{1}, b_{1}, c_{1})$ a $(a_{2}, b_{2}, c_{2})$ , 3D vektory v tělese $K$ . Oba nenulové.

Jelikož oba nejsou násobky toho druhého, jsou lineárně nezávislé. Takže matice

$((a_{1}, b_{1}, c_{1}), (a_{2}, b_{2}, c_{2}))$

má rank 2. Jukněme na sloupce jako 2D vektory. Víme že 3 vektory v 2D prostoru musí být lineárně závislé. Takže existují 3 čísla $x, y, t \in K$ taková že ne všechny najednou jsou 0 kde:

$x (a_{1}, a_{2}) + y (b_{1}, b_{2}) + t (c_{1}, c_{2}) = (0, 0)$

Pokud toto přepíšeme pro každou souřadnici zvlášť, dostaneme že bod $(x, y, t)$ leží na obou přímkách!! (z definice ležení na přímce)

Zároveň ale protože rank matice je 2, musí existovat 2 lineárně nezávislé sloupce. Búno to jsou $(a_{1}, a_{2})$ a $(b_{1}, b_{2})$ . To znamená že pro libovolný vektor $(u, v)$ má $x (a_{1}, a_{2}) + y (b_{1}, b_{2}) = (u, v)$ unikátní řešení.

Takže pokud se koukneme na tamtu rovnici znova:

$x (a_{1}, a_{2}) + y (b_{1}, b_{2}) + t (c_{1}, c_{2}) = (0, 0)$

pak první 2 čelny jsou zašpendlíkované na místě a jediná vůle je v posledním členu když ho škálujeme $t$ čkem. ALE to znamená že rovnice může vycházet jen pro jednu hodnotu $t$ !

Pozorování

2 body sdílí právě 1 přímku

Důkaz

stejně jako 2 přimky sdílí 1 bod

Pozorování

existují 4 body takové že každá přímka protne max 2

Důkaz

Třeba: $(0, 0, 1), (0, 1, 0), (1, 0, 0), (1, 1, 1)$ i think

Latinský čtverec

Definice: Latinský čtverec řádu

n

čtvercová tabulka $n$ řádků a $n$ sloupců. V každém políčku je jedno číslo od $1$ do $n$ .

Každé číslo se objevuje právě jednou v každém sloupečku a právě jednou v každém řádku.

Definice: Ortogonalita latinského čtverce

Když vezmu 2 a transparentně je položím na sebe, v každém z $n^{2}$ políček dostanu dvojici čísel. Tyto 2 LČ jsou ortogonální pokud se žádná dvojice nezopakuje.

(Jelikož dvojic je $n^{2}$ , každá dvojice se ve skutečnosti musí objevit právě jednou)

Pozorování

Počet ortogonálních latinských čtverců řádu $n$ je maximálně $n - 1$

Důkaz

Nejprve pozorování: Budiž ortogonální latinské čtverce $A$ a $B$ oba řádu $n$ a $π$ permutace čísel $1, 2, \dots, n$ .

Vyrobíme nový latinský čtverec $A'$ . Ten bude mít na pozici $(i, j)$ číslo $π (a_{i j})$ (kde $a_{i j}$ je pozice $(i, j)$ v LČ $A$ ).

Po rozmyšlení je vidět že i $A'$ je ortogonální k $B$ . Tudíž:

Pozorování

Ortogonalita LČ se nezmění přejmenováním symbolů v jednom z nich.

Představme si latinské čtverce $A_{1}, A_{2}, \dots, A_{t}$ každé 2 z nich ortogonální.

Pro každé $A_{i}$ : permutujme jeho symboly tak aby měl na prvním řádku bylo $1, 2, \dots, n$ .

Podle pozorování víme, že i tyto $A'_{1}, A'_{2}, \dots, A'_{t}$ jsou každý s každým ortogonální.

Jukněme, co může být na pozici $(2, 1)$ některého $A'_{i}$ :

určitě ne $1$ . Ta už je ve stejném sloupci na $(1, 1)$ .
žádné 2 $A'_{i}, A'_{j}$ tam nemůžou mít stejné číslo. Kdyby tam měli stejné číslo, jejich dvojice by na $(2, 1)$ měla dvojici $(k, k)$ ale ta se už objevila na $k$ tém místě prvního řádku! tudíž $2, 3, \dots, n$ mohou být na pozici $(2, 1)$ pouze v jednom $A'_{i}$ takže $t \leq n - 1$ . 🔲

Pozorování

Pro $n \geq 2$ existuje FPR řádu $n$ pokudd existuje $n - 1$ navzájem ortogonálních LČ řádu $n$ .

Důkaz

Nejprve sestrojíme FPR řádu $n$ z $n - 1$ navzájem ortogonálních LČ řádu $n$ .

Jako template vezmem fancy tvar:

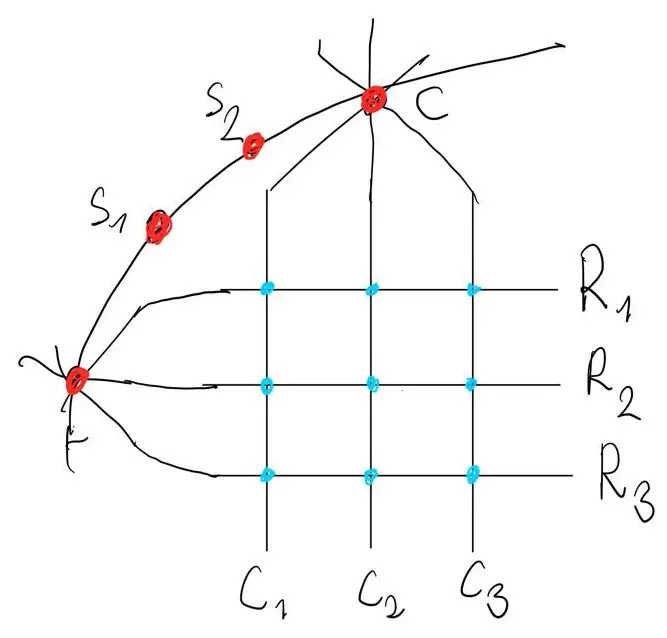
a teď si všimni že tam je dost bodů ale málo čar. Takže podle těch LČ které jsme stále nepoužili budeme proplétat nové přímky tím gridem vpravo dole.

Pro každé $m \in {1, 2, \dots, n}$ a $k \in {1, 2, \dots, n - 1}$ vyrobíme přímku:

$L_{k m} = {s_{k}} \cup {(i, j) | {(S_{k})}_{i j} = m}$

Tzn: Začneme přímku v $s_{k}$ a tam kde má LČ $k$ políčko s číslem $m$ appendneme do přímky.

Tohle je určitě FPR (důkaz vymysli na místě). Jde provést pozpátku pro vytvoření LČ z FPR. Stačí vybrat $r$ a $c$ libovolně.🔲

Numberphile video about M.O.L.S.

Toky v sítích

Takovej speedrun protože to určitě umíme.

Definice: Síť + tok

Síť je čtveřice $(G, s, t, c)$ . $G$ je graf (dvojice množiny vrcholů a relace), $s$ a $t$ jsou vrcholy (source a sink) a c je funkce z hran do $[0, + \infty]$ .

Tok je pak funkce $f$ která dává hranám ohodnocení.

Pravidla pro toky:

$f (e) \leq c (e)$ - nemůžu hraně dát víc než co se do ní vejde
$\forall v \in V (G) \ {s, t} : \sum_{(x, v) i n E (G)} f (x, v) = \sum_{(v, y) i n E (G)} f (v, y)$ , neboli do vrcholu teče stejně jako odtéká [P: chapter 4.1, 4.2, 4.3]

$v a l (f)$ je velikost toku, třeba přebytek ve stoku

Pozorování

Každá síť má maximální tok - sketch, asi přes rozbor algoritmu xd

Definice: Řez

Řez je množina hran po jejichž odstranění se graf rozpadne na více komponent

Definice: Elementární řez (partition)

Je to vlastně to samý, ale komponenty musí být 2. Obv zdroj je v A a stok je v B. $v a l (f) = f (A, B) - f (B, A)$

Pozorování

elementární řez je taky řez a
Každý řez obsahuje elementární řez.

Důkaz

Takový hrátky z cestami. v (i) si pořidíme cestu z $s$ do $t$ a říkáme, že jedna z hran této cesty je v řezu. To je vidět, protože $s$ a $t$ jsou v jiných komponentách.

ve (ii) je to to samé. Máme řez $R$ . Pořídíme $A$ a $B$ , A bude množina vrcholů do kterých se dá dostat v $G - R$ z $s$ a $B$ bude její doplněk. Pak tvrdíme že $S (A, B) s u b s e t R$ . Kdyby nebyl, tak existuje hrana v $(x, y) \in S r$ , $x \in A$ a $y \in B$ . Pak ale cesta do y nekřižuje R, tedy je ve stejné komponentě jako $s$ a tedy musí být v $A$ .

Ano, je to kokotina.

Pozorování

$v a l (f) \leq c (R)$

Důkaz

Zadefinujeme přebytek na vrcholu -tj. rozdíl mezi přítokem a odtokem. Tento rozdíl je pak roven $f^{Δ} (A, B) = \sum_{v i n B} f^{Δ} (v) = f^{Δ} (t)$ . První rovnost rozborem případů kudy vede hrana, druhá rovnost je triviální - všechny vrcholy mají přebytek 0.

Zlepšující hrany (augmenting path), věta o tom že maximální tok je roven minimálnímu řezu. [P 4.2.5], známe z primy.

Ford-Fulkerson algoritmus hledá cesty v síti rezerv. Když ji najde, tak ji přičte do toku. Na celočíselných hranách se zastaví a vydá maximální tok. (bez důkazu)

[P: chapter 4.4, 4.5]

Definice: Systém různých reprezentantů

Nechť $M$ je konečný systém konečných množin. Nechť $N$ je sjednocení všech množin $m \in M$ . Potom funkci $f : M \to N$ nazveme systém různých reprezen- tantů právě tehdy, když je prostá a současně $\forall m \in M : f (m) \in m$ .

Definice: Párování

Buď $G = (V, E)$ graf a buď $M \leq E$ množina dvojic vrcholů $G$ . Pak $M$ nazveme párování v grafu $G$ právě tehdy, když je každý vrchol $G$ v nejvýše jedné dvojici v $M$ .

Věta: Hallova

Nechť $M$ je konečný systém konečných množin. Pak platí, že $M$ má systém různých reprezentantů právě tehdy, když pro každou $F \subseteq M$ a sjednocení všech jejích prvků $u u F$ platí $| u u F | \geq | F |$ .

Věta: Hallova, bipartitní formulace

Nechť G = (V, E) je bipartitní graf s parti tami X a Y . Pak má G párování obsahující všechny vrcholy partity X právě tehdy, když pro každou M ⊆ X platí, že z ní vedou hrany k alespoň |M | různým vrcholům Y.

DŮ

Pozorování

König-Egerváry theorem

Velikost maximálního párování v bipartitním grafu je rovna minimální velikosti vrcholového pokrytí (proof ommited, ale docela obvious). N

Defect Hall theorem
Existence of a perfect matching in a regular bipartite graph

Grafová souvislost

[P: chapter 5.1, 5.2]

Definice: Vrcholová souvislost

k_{v} (G)

Pokud $G$ je $K_{n}$ pak to je $n - 1$ JINAK

$k_{v} (G)$ je velikost nejmenšího vrcholového řezu $A$ .

Definice: Hranová souvislost

k_{e} (G)

$k_{e} (G)$ je velikost nejmenšího hranového řezu.

Definice: Hranově/Vrcholově souvislý

$G$ je hranově/vrcholově $k$ -souvislý pokud $k_{e ⁄ v} (G) \geq k$ .

Pozorování

Pro graf $G$ s alespoň 2 vrcholy:

$(\forall e \in E (G)) (k_{e} (G) - 1 \leq k_{e} (G - e) \leq k_{e} (G))$

“Odebráním libovolné hrany se $k_{e}$ může jedině snížit a to maximálně o 1”

$(\forall F \subseteq E (G)) (k_{e} (G - F) \leq k_{e} (G))$

“Odebráním libovolné množiny hran se $k_{e}$ může jedině snížit”

Důkaz

To první jistě plyne z toho druhého

Pozorování

$k_{e} (G)$ se po odebrání hrany sníží maximálně o 1 ( $k_{e} (G - e) \geq k_{e} (G) - 1$ )

Důkaz

Vezmeme $k_{e} (G) - 2$ velkou $F \subseteq E (G - e)$
Pak $F' = F \cup {e}$ .
Takže $| F' | \leq k_{e} (G) - 1$ .

Z toho plyne že $(G - e) - F$ je spojitý. ale $| F' |$

$k_{e} (G) - 1 \leq k_{e} (G - e) \leq k_{e} (G)$
$k_{v} (G) - 1 \leq k_{v} (G - e) \leq k_{v} (G)$
$k_{v} (G) \leq k_{e} (G)$
Ford-Fulkerson theorem: A graph is k-edge-connected iff for every 2 vertices there exist k edge-disjoint paths
Menger theorem: A graph is k-vertex-connected iff for every 2 vertices there exist k vertex-disjoint paths (stated).
bonus: Another notion to measure how well connected a graph is: expansion

Graph connectivity cont’d and double counting

[P: chapter 5.3] and [P: chapter 6.3, 6.4]

bridge, articulation, edge subdivision
subdividing an edge of a vertex-2-connected graph preserves vertex-2-connectivity
Ear lemma

Pozorování

Graf je vrcholově 2-souvislý právě tehdy když zle sestrojit z cyklu kterému přilepujeme uši. (Ear lemma, ušní lema, ušizmus)

Důkaz

$\Rightarrow$ :

Cyklus je jistě vrcholově 2-souvislý. Přidáním ucha nemůže vzniknout vrchol takový že po jeho odebrání se graf rozpadne.

$\Leftarrow$ :

Budiž graf $G$ který je vrcholově 2-souvislý. K němu vyrobíme co největší podgraf $H$ který jsme vytvořili z cyklu a přilepování uší.

Tvrdím, že $H$ je indukovaný podgraf. Pokud ne, pak existuje dvojice vrcholů mezi kterýma nevede hrana v $H$ ale vede hrana v $G$ . Pak ale $H$ není největší možný. Tudíž $H$ musí být indukovaný.

Předpokládám že existuje vrchol, který je v $G$ ale není v $H$ . Jelikož $G$ je souvislý. Musí existovat dvojice vrcholů $u$ , $v$ která sousedí a $u$ je v $H$ ale $v$ ne.

Jelikož je $G$ vrcholově 2-souvislý, po odebrání $u$ se nemůže rozpadnout. Tudíž stále existuje cesta z $v$ do $u$ . To je ale ucho které jsme měli přidat takže všechny vrcholy $G$ jsou v $H$ .

Jelikož $H$ a $G$ mají stejné vrchly a jelikož $H$ je indukovaný podgraf, musí to být stejné grafy. 🔲

Cayley’s formula for the number of spanning trees of a complete graph (proof due to Pitman by double-counting, see e.g. Wiki)
Exercise: #spanning trees of a $K_{n}$ minus one edge (stated).
Sperner theorem about the size of the largest antichain in $P ([n])$
Graphs without a $C_{4}$ subgraph have $O (n^{\frac{3}{2}})$ edges (stated)
bonus riddle (Erdős-Ko-Rado theorem): How many subsets of size 5 can you choose from ${1, 2, ., 10}$ so that every 2 of them intersect?

Ramseyho teorie

Když máme dost velkou hromadu věcí tak v ní musí být nějaká struktura - Pepík

(syntax shugar: $[n] \overset{def}{=} {1, 2, \dots, n}$ )

Pozorování

Pigeonhole principle

Množina $[1 + n_{1} + n_{2} + \dots + n_{t}]$ kde každý prvek je obarvený jednou z $t$ barev.

Pak existuje barva $i$ která se objeví $\geq n_{i} + 1$ -krát

Důkaz

Pokud ne, pak je obarveno jen $\leq n_{1} + n_{2} + \dots + n_{t}$ koulí.

Pozorování

6-členná party

Pokdu obarvíme hrany $K_{6}$ červeně a modře, pak existuje jednobarevný trojúhelník.

Důkaz

(Note: nefunguje pro $K_{5}$ . (pentagon s hvězdou uprostřed))

Vem vrchol. Koukni na 5 odchozích vrcholů. 3 z nich musí mít stejnou barvu BÚNO červená.

Teď jukni na tyhle 3 vrcholy. Můžou se stát 2 věci:

Nějaké 2 mají taky červenou hranu mezi sebou takže výhra
žádné 2 nemají červenou hranu mezi sebou takže! všechny 3 mají mezi sebou modrou hranu, což tvoří modrý trojúhelník.

Definice: Ramseyho číslo

R (k, l)

$R (k, l)$ je nejmenší možné číslo takové, že kdykoliv obarvujeme hrany grafu $K_{R (k, l)}$ červeně a modře, pak existuje buď:

podgraf $K_{k}$ kde jsou všechny hrany červené NEBO
podgraf $K_{l}$ kde jsou všechny hrany modré.

(Poznámka: graf ve kterém hledáme musí být úplný. Grafy které hledáme musí být úplné)

Note: $R (3, 3) = 6$ (6-členná party)

Pozorování

(Ramsey pro hrany a 2 barvy)

$(\forall a, b \geq 1) (R (a, b) \leq ([a - 1 + b - 1], [a - 1]))$

Důkaz

Indukcí po $a + b$ .

Init: pro $a = 1$ nebo $b = 1$ pak $K_{1}$ funguje haha. (bo $K_{1}$ má 0 hran takže pro ně platí všechno)

Indukční předpoklad:

$R (a - 1, b) \leq ([a - 2 + b - 1], [a - 2])$
$R (a, b - 1) \leq ([a - 1 + b - 2], [a - 1])$

Budiž $n = R (a - 1, b) + R (a, b - 1)$ a vem $K_{n}$

Teď to přepíšeme aby to vypadalo holubníkovitě:

$n - 1 = \underset{Jedna extra hrana}{\underset{⏟}{1 +}} (R (a - 1, b) - 1) + (R (a, b - 1) - 1)$

Vem $v$ , vrchol $K_{n}$ , a zase jukni na jeho hrany. Holub tvrdí že bude:

$\geq R (a - 1, b)$ červených hran NEBO
$\geq R (a, b - 1)$ modrých hran.

Pokud 1. pak z předpokladu víme že:

buď červený sousedi obsahují červenou $K_{a - 1}$ , pak po přidání $v$ dostaneme červenou $K_{a}$
nebo červený sousedi obsahují modrou $K_{b}$ , pak yay.

Jinak 2. pak analogicky pro modré sousedy.

Pozorování

lower bound $R (k, k)$

$(\forall k \geq 3) (R (k, k) > 2^{\frac{k}{2}})$

Důkaz

Chňapni $K_{n}$ kde $n \leq 2^{\frac{k}{2}}$ a obarvi všechny hrany nezávisle.

Tohle nemusí fungovat obv ALE

Jak často se stane, že když vyberu množinu $X$ o $k$ vrcholech pak mají všechny stejnou barvu? well this: ${(\frac{1}{2})}^{([k], [2])} + {(\frac{1}{2})}^{([k], [2])}$

Jaká je šance že nějaký $k$ -prvková množina vrcholů má všechny hrany stejné? well $\leq$ než počet $k$ -prvkových množin $\cdot P_{fail}$

něco něco idk nemám rád pravděpodobnost

IF YOU HAVE A SUFFICIENT AMOUNT OF BALLS

Definice:

([x], [p])

Budiž množina $X$ a $p \in ℕ$ .

$([x], [p])$ je množina všech $p$ -prvkových podmnožin $X$ .

Pozorování

Nekonečná verze Ramseyovy věty pro hypergrafy (bro jestli tohle nezní cool tak idk)

Pro libovolné obarvení $([ℕ], [P])$ pomocí $t$ barev (barva je vlastnost podmnožiny)

existuje nekonečná množina $A \subseteq ℕ$ kde $\forall Q \in ([A], [P])$ dostanou stejnou barvu.

Důkaz

Indukce podél $p$ . Pro $p = 1$ , barvíme $ℕ$ pomocí $t$ barev, takže nějaká barva se objeví nekonečně mnoho krát.

Řekněme že pro $p$ , vem $p + 1$ .

Nechť $C : ([ℕ], [p + 1]) \to [t]$ je barvení všech $(p + 1)$ -tic pomocí barev $1, 2, \dots, t$ .

postavíme podmnožiny $A_{1} \supseteq A_{2} \supseteq A_{3} \supseteq \dots$ kde $A_{1} = ℕ$ a $v_{1}, v_{2}, \dots \in ℕ$ kde $v_{1} = 1$ .

Pak předpokládáĺe že už máme $A_{1}, A_{2}, \dots, A_{i}$ a $v_{1}, v_{2}, \dots, v_{i} \in ℕ$ . Definujeme $c' : ([A_{i} ?], [p])$ přiřazením barvy $c (Q \cup)$ té $p$ -tici $Q$ .

Indukcí, najdi nekonečnou podmnožinu $A_i+2 sube A_i$ tak že všechny
$p$-prvkové podmnožiny dostanou stejnou barvu.

Pozorování

König lemma (O nekonečných stromech)

(důkaz nebude ve zkoušce)

Pokud $T$ je nekonečný strom se všemi stupni konečnými.

Čapni libovolný vrchol. Pak existuje nekonečná cesta po $T$ z tohoto bodu.

(jakože lol obviously wtf)

Důkaz

(sketch) Vem vrchol $x_{0}$ jako kořen. ten má konečně mnoho sousedů. Jukněme na ně. Součet jejich velikostí je nekonečno. takže alespoň jeden ze sousedů musí být nekonečný strom. takže půjdeme tam. Ez done

Vibe: A teď tohle umí spoutat konečné a nekonečné struktury

Pozorování

Ramsey pro hypergrafy, konečný (still cool)

Vem $p, t, k_{1}, \dots, k_{t} \in ℕ$ . Pak existuje konečné číslo $R_{p} (\begin{matrix} k_{1} & \dots \\ k_{t} \end{matrix})$ takové že kdykoliv obarvujeme $(([n]), [p])$ kde $n \geq R_{p} (k_{1}, \dots, k_{t})$ pak

#(Dec 17): Ramsey theory, cont’d [P: chapter 7.3].:

Věta: Happy ending problem

Pro jakoukoliv množinu pěti bodů v rovině v obecné poloze (ne 3 na přímce) tvoří alespoň jedna čtveřice konvexní čtyřúhelník.

Důkaz

Vezmeme kovexní obal (covex hull) těchto pěti bodů. (i) Pokud je to pětiúhelník -> jakékoliv 4 dělají konvexní čtyřúhelník. (ii) Pokud je to čtyřúhelník, tak ty čtyři na okraji Předpokládejme tedy že obal je trojúhelník. Ostatní dva body nemůžou ležet na jeho okraji (obecná poloha), ale uvnitř.

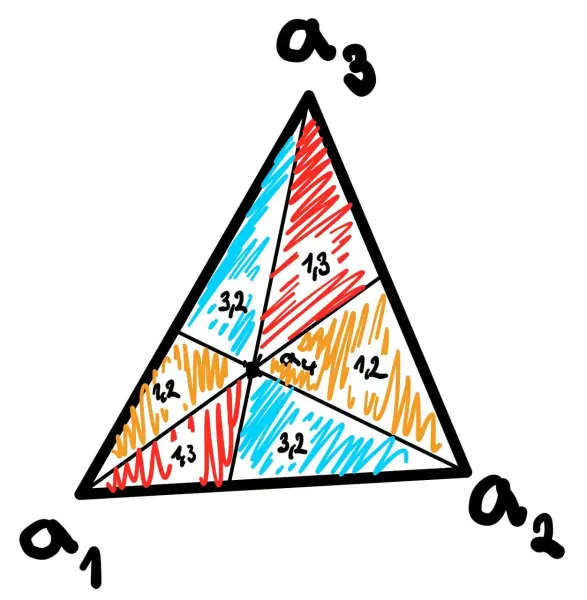
Vezmeme tedy jeden a postavíme 6 částí jako na obrázku. Podle toho v jaké části leží $a_{5}$ vybereme zbývající dva vrcholy trojúhelníku společně s $a_{4}$ a máme hotovo. $a_{5}$ opět nemůže ležet mezi částmi, kvůli obecné poloze.

Věta: Erdős-Szekeres theorem

Pro $t \geq 4$ , jakákoliv mnozina $R^{4} (5, t)$ bodů v rovině v obecné poloze obsahuje alespoň $t$ bodů tvořící konvexní čtyřúhelník.

Důkaz

Pořídíme si množinu $S$ $R^{4} (5, t)$ bodů v rovině. V ní obarvíme všechny čtveřice $c : ([S], [4]) \to [2]$ tak, že

$c (X) = 1$ , tak netvoří konvexní čtyřúhelník
$c (X) = 2$ , tak tvoří konvexní čtyřúhelník

Množství bodů (Ramseyovo číslo) nám teď říká, že:

existuje pětice taková, že každá čtveřice z pětice má barvu 1 NEBO
existuje t-tice taková, že každá čtveřize z t-tice má barvu 2.

První případ se nemůže stát, je to přímá negace Happy-ending problému. Takže určitě existuje nějaká t-tice $A_{2}$ , ve které $\forall X \in ([A_{2}], [4]) : c (X) = 2$ . Vezměme konvexní obal této $A_{2}$ . Pokud má t vrcholů, tak jsme vyhráli. Pokud má měné než t vrcholů, tak existuje nějaký vrchol $z$ , co je uvnitř. To znamená že existují nějaké body $x_{1}, x_{2}, x_{3}$ které tvoří trojúhelník ve kterém je $z$ uzavřeno.

Tato čtveřice bodů ale netvoří čtyřúhelník, což je spor, protože mají barvu 2.

Error-correcting codes

[P: chapter 8]

Motivační příklad. Pojďme si posílat zprávy. Komunikační linka je ale nestabilní a mění nám znaky za jiné. Chtěli bychom za málo poslaných znaků navíc dokázat opravit co nejvíce takto změněných znaků.

Pro jednoduchost pojďme posílat bity. Náš jazyk má tedy pouze dva znaky. Abychom, dokázali opravit nějakou chybu, každý bit co pošleme ztrojíme. Místo “1101” pošleme “111111000111”. Jakýkoliv změněný bit dokážeme opravit, protože druhé dva ve trojici zůstanou nezměněny. Pokud ale někdo změní dva bity, můžeme mít smůlu a kód opravit špatně.

Definice: Primitivy

abeceda (alphabet) je konečná množina znaků $Σ = {s_{0}, \dots, s_{m}}$ - abeceda často bude nějaké konečné těleso, nejčastěji $F_{2}$
slovo délky $n$ je seznam (nebo řádkový vektor) $n$ znaků z abecedy
$Σ^{n}$ je množina všech slov délky $n$ z abecedy $Σ$
kód $C$ je podmnožina $Σ^{n}$ .
prvky kódu jsou codewords, for the lack of neat translation

Definice: Hammingova vzdálenost

Je to jednoduše počet rozdílných znaků ve dvou slovech. Formálně $\forall x, y \in Σ^{n}, d (x, y) \overset{def}{=} | {i \in {1, \dots, n} | x_{i} \neq y_{i}} |$ Rozmysli si, že je to metrika na $Σ^{n}$ .

Definice: Hamming weight (váha?)

Je definovaná jako počet “nenulových” znaků, nebo Hammingova vzdálenost od nulového vektoru.

Jak se tyto primitivy používají?

S je odesílatel, R je přijímač. S i R znají nějakou bijekci $π$ mezi všemy kódy $C s u b s e t Σ^{n}$ a všemi možnými zprávami. Je to bijekce, tedy množina kódů a všech zpráv jsou stejně velké. Všechny zprávy budou tipicky kratší než n, jinak by to byl docela naprd kód.

S tedy vezme zprávu, přeloží ji na kód a pošle R. R zprávu přijme, možná s nějakými chybami. Opraví ji a pomocí $π^{- 1}$ ji přeloží zpátky na zprávu.

Definice:

{(n, k, d)}_{q}

kód

Předpokládejme abecedu o alespoň dvou znacích a C je kód s alespoň dvěma codewords. Tento kód má pak nějaké parametry.

$n$ = délka slov v $C$
$q$ = velikost abecedy ( $| Σ |$ )
$k$ = velikost $C$ je $| C |$ , užitečnější ale bude logaritmus o základu q. $k = \log_{q} a b s (C)$
$d$ = minimální vzdálenost v $C$ ( $\min ({d (x, y | (x, y \in C) (x \neq y)})$ )

To nám dává ${(n, k, d)}_{q}$ kód. Rozmysli si, kolik dokážeme v takovém kódu opravit chyb.

řešení $⌊ \frac{d - 1}{2} ⌋$

Příklady kódů. Náš opakující se kód ze začátku byl ${(n, 1, n)}_{q} - k ó d$ , kde n je “činitel” (slova jsou roznásobené znaky). Slova jsou dlouhá $n$ , to si můžeme zvolit jak chceme. Množina kódů je stejně velká jako abeceda, protože akorát vezme každý znak z abecedy a dá ho $n$ krát za sebou. $k$ je tedy 1, protože je to $\log_{q} (q)$ . Minimální vzdálenost bude přesně $d = n$ , protože každá dvě slova jsou kompletně jiná.

Rozmysli si, co je za kód co nic nedělá. Pouze pošle slovo nad nějakou abecedou $Σ$ velikosti $q$ délky $n$ . Nijak ho nepřeloží.

Hint: $n$ je zadané, $k = \log_{q} (| C |)$ -> kolik je $| C |$ ? $d =$ minimální vzdálenost dvou kódů.

Řešení: ${(n, n, 1)}_{q}$ . To protože kódů je $q^{n}$ - jsou to všechny zprávy. Vzdálenost dvou kódů je malá, pouze 1.

Parity code. $q = 2$ a naše kódy budou mít vždy součet $= 0$ nad $ℤ_{2}$ . Tento kód bude ${(n, n - 1, 2)}_{2}$ kód. $| C | = 2^{n - 1}$ , prvních $n - 1$ znaků si můžeme vybrat a poslední určíme tak, aby byl součet co nejmenší. $k = \log_{2} (2^{n - 1}) = n - 1$ . Vzdálenost $d$ je 2, protože dva kódy nemůžou mít vzdálenost 1, to by znamenalo že jeden z nich má součet $= 1$ .

Teďka se řeší nějaký boundy na to, jak velký můžou bejt ty množiny kódů (jakoby $k$ ), když nám někdo zadá n,d,q. Upřímně doufám že to ommitne protože to sou fakt hovna xd.

Definice: Singleton bound, Hamming bound, Gilbert-Varshamov bound,

ommited by Džanek, read up on [P 8.3]

Definice: Linear codes

Lineární kód je podprostor prostoru $Z_{q}^{n}$ . Pokud je to také ${(n, k, d)}_{q}$ kód, tak se píše do hranatých závorek, je totiž důležitej :)

Těmi kódy co posíláme jsou opravdu myšleny vektory toho podprostoru. Čím větší si vezmu, tím má větší dimenzi a tím se mi zvětšuje $k$ . Ale kvůli tomu bude menší $d$ . Ještě existuje pojem generator matrix - to jsou bazické vektory $C$ nasázené do sloupce. Z toho se dá vyrobit parity check - to je taky matice, ale tentokrát báze kolmých vektorů.

Vynásobením $x H$ lze jednoduše ověřit, jestli $x$ do C patří, či nikoliv.

Pozorování

Pokud je $C$ an ${[n, k, d]}_{q}$ -kód, tak $\dim (C) = k$

Důkaz

Pořiďme si $l \overset{def}{=} \dim (C)$ . ${c_{1}, \dots, c_{l}}$ jsou bazické vektory $C$ . $C$ je nyní složené z lineárních kombinací těchto vektorů $\sum_{i = 0}^{l} a_{i} c_{i}$ . Pro každé $a_{i}$ máme $q$ možností jak si vybrat (protože $| F_{q} | = q$ ). Jelikož jsou vektory lineárně nezávislé, tak je celkem $q^{l}$ různých kódů.

Z toho $k = \log_{q} (q^{l}) = l$ 🔲

Pozorování

Pokud je $C s u b s e t F_{q}^{n}$ ${[n, k, d]}_{q}$ - kód s $0 < k < n$ , tak

$d = \min {w t (x | x i n C \ {0}}$

wt je Hammming weight - vzdálenost od 0.

Důkaz

Zafixujeme $x \neq 0$ s nejmenší hammingovskou váhou. Dokazujeme že $d = w t (x)$ .

Jelikož $C$ je kód ve kterém je 0 i x, tak $d (x, 0) = w t (x) \geq d$ z definice d - je nejmenší takové. V $C$ také existují různé vektory $y, z$ , jejichž $d (y, z) = d$ . Jelikož $C$ je podprostor, tak $y - z \in C$ . Tudíž $w t (x) \leq w t (y - z)$ - to víme protože x je nejmenší takové.

Celkově $d = d (y, z) = w t (y - z) \geq w t (x)$ . Složením nerovností 🔲.

Definice: Hamming bound

Když fixneme $n$ a $d$ tak $k$ musí být small.

(wait je tohle hamming code?)

$C sube Z_2^n je $(n, k, d = 2 t + 1)$ pak $| C | \leq \frac{2^{n}}{V (t)}$ .

Důkaz

Pro každé $x \in C$ jukni na kouli $B_{n} (x, t)$ . Protože $C$ má $d = 2 t + 1$ , žádné 2 koule se nepřekrývají.

(slova, slova … důkaz že se nepřekrývají)

pak $| C | > \frac{n^{2}}{V (t)}$ protože velikost prostoru je $2^{n}$ a $V (t)$ je volume koule a pokud se nepřekrývají tak něco něco

Gilbert-Varnshmdr Bound

$\forall v, d \geq 1 \exists C \in ℤ_{2}^{n} w i t h Δ (c) = d$ and $| C | \geq \frac{2^{n}}{V (d - 1)}$

Zdroje

I. Penev: Combinatorics and Graph Theory 1 & 2
J. Matoušek, J. Nešetřil: Invitation to discrete mathematics, 2nd edition, 2008 👈 tenhle je fakt good
Tomáš Sláma (goat)
the voices in my head

uuuuwwwiieee